浙大数据结构的编程题——03-树的同构
03-树1 树的同构 (25 分)
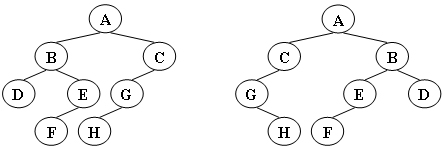
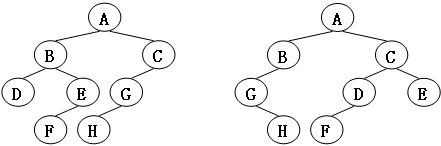
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
图1
图2
现给定两棵树,请你判断它们是否是同构的。 输入格式: 输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例1(对应图1):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例1:
No
思路
此题在Mooc上有详细讲解。大概流程是,输入用结构数组表示二叉树,而实现静态链表。将树的结构存储下来。
而同构判别部分使用了递归的思路。详细求解思路请看Mooc.
Code
#include <iostream>
#include <string>
#include <vector>
#include <list>
#include <map>
#include <algorithm>
#include <iterator>
#include <math.h>
#include <stack>
using namespace std;
struct Node
{
char Data;
int leftNode, rightNode;
};
int builtTree(vector<Node> &tree, unsigned int N) {
int sum = 0;
int root = -1;
for (int i = 0; i < N; i++) {
char cl, cr;
scanf("%c %c %c\n", &tree[i].Data, &cl, &cr);
if (cl == '-') {
tree[i].leftNode = -1;
}
else {
tree[i].leftNode = cl - '0';
sum += cl - '0';
}
if (cr == '-') {
tree[i].rightNode = -1;
}
else {
tree[i].rightNode = cr - '0';
sum += cr - '0';
}
root = (0 + N - 1)*N / 2 - sum;
}
return root;
}
int isOmorphic(int R1, int R2, vector<Node> &T1, vector<Node> &T2) {
if ((R1 == -1) && (R2 == -1)) return 1;//both empty
if ((R1 == -1) || (R2 == -1)) return 0;
if (T1[R1].Data != T2[R2].Data) return 0;
//当前节点已无问题,检查子节点,递归调用。
int T1l = T1[R1].leftNode, T1r = T1[R1].rightNode;
int T2l = T2[R2].leftNode, T2r = T2[R2].rightNode;
if ((T1l == -1) && (T2l == -1)) return isOmorphic(T1r, T2r, T1, T2);
if ((T1l != -1) && (T2l != -1)) {//left and right both exist
if (T1[T1l].Data == T2[T2l].Data) return isOmorphic(T1l, T2l, T1, T2) && isOmorphic(T1r, T2r, T1, T2);
}
return isOmorphic(T1l, T2r, T1, T2) && isOmorphic(T1r, T2l, T1, T2); //交换左右子节点
}
int main() {
//begin:17:06 end:
//ios::sync_with_stdio(false);
vector<Node> tree1(10), tree2(10);
unsigned int N;
scanf("%d\n", &N);
int root1 = builtTree(tree1, N);
scanf("%d\n", &N);
int root2 = builtTree(tree2, N);
if (isOmorphic(root1, root2, tree1, tree2) == true) {
printf("Yes\n");
}
else {
printf("No\n");
}
return 0;
}
并查集的方法
SAquarius 指出了一种用关联容器存储所有的结点的父子关系,当两颗树具有完全相同的父子关系时,即为同构。代码如下:
感谢SAquarius 指出更高效的实现方式。
//用并查集更简单直观一点,读入的时候创建并查集,然后,用map容器直接记录每个结点的父节点
//这样不用左右子树考虑那么多种情况,因为同构的时候父子关系是不变的,变得只是左右位置,直接判定父子关系就行了
//这样直接用两个map容器是否相等就直到两个树是不是同构
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>
#include<algorithm>
#include<map>
#include<unordered_map>
#include<vector>
#include<queue>
#include<stack>
#include<string>
using namespace std;
typedef struct{
char data;
int fa;
}Node;
map<char,char> mp1;
map<char,char> mp2;
void CreatTree(map<char,char> &mp);
int main(){
#ifdef ONLINE_JUDGE
#else
freopen("1.txt", "r", stdin);
#endif
CreatTree(mp1);
CreatTree(mp2);
if(mp1==mp2)
puts("Yes");
else
puts("No");
return 0;
}
void CreatTree(map<char,char> &mp)
{
int n;
char a,b,c;
cin>>n;
vector<Node> v(n);
getchar();
for(int i=0;i<n;i++){
v[i].fa=-1;
}
for(int i=0;i<n;i++){
scanf("%c %c %c",&a,&b,&c);
getchar();
v[i].data=a;
if(b!='-') v[b-'0'].fa=i;
if(c!='-') v[c-'0'].fa=i;
}
for(int i=0;i<n;i++){
int index=v[i].fa;
if(index==-1)
mp[v[i].data]='#';
else
mp[v[i].data]=v[index].data;
}
}